Wird man im Regen nasser, wenn man läuft oder steht?
In den folgenden Bildern regnet es Bindfäden.
Die Frage ist: Wird man nasser oder bleibt man trockener, wenn man, statt zu stehen, durch den Regen rennt?
Eine anschauliche Lösung findet sich in den beiden Bildern:
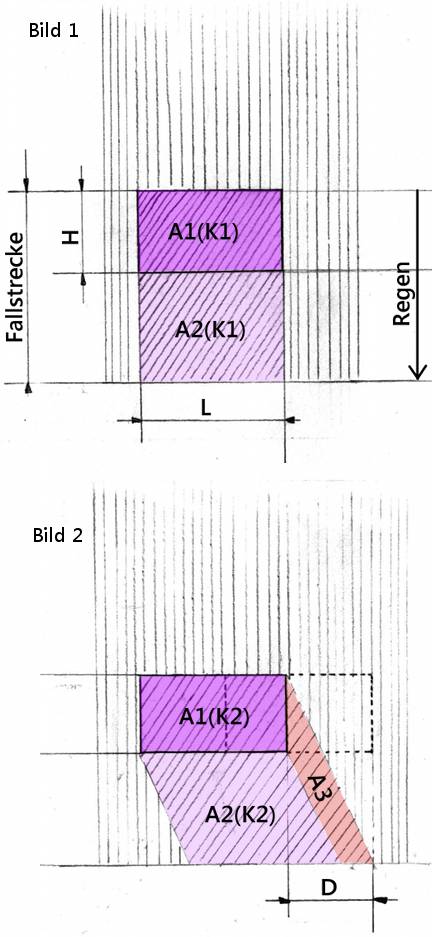
Das obere Bild 1 zeigt die Situation mit stehendem Körper, das untere Bild 2 zeigt das ganze mit einem bewegten Körper. Eingezeichnet sind die "Regenschatten", die die jeweiligen Körper hinterlassen. Die Fläche dieses Regenschattens entspricht der Menge des "abbekommenen" Regens.
Die Körper (Höhe:H, Länge:L) sind die dunkelvioletten Rechtecke. Der Regen ist in seinem Fall durch die senkrechte Straffur dargestellt. Die sich ergebenden Abschattungen sind schrägschraffiert eingezeichnet.
Der Körper in oberen Bild 1 steht in der betrachteten Zeit (t) unbeweglich im Regen. Im unteren Bild 2 bewegt sich der Körper in der gleichen Zeit um die Wegstrecke D. Der Regen fällt in ebenjener Zeit die Wegstrecke Fallstrecke (oben wie unten).
Die Schattenfläche des stehenden Körpers in Bild 1 entspricht den Flächen A1(K1) + A2(K1).
Im Fall des bewegten Körpers aus Bild 2 ergibt sich die Schattenfläche aus "A1(K2)" + "A2(K2)" + "A3".
Wie leicht zu erkennen ist, sind die Größen der violetten Flächen (A1,A2) in beiden Bildern identisch. In Bild 2 ist in der Gesamtabschattungsfläche jedoch zusätzlich noch die Fläche "A3" enthalten. Die Abschattungsfläche des bewegten Körpers ist also größer als die des stehenden Körpers.
Das wäre also geklärt: Man wird nasser, wenn man sich im Regen bewegt ...
Die Frage ist: Wird man nasser oder bleibt man trockener, wenn man, statt zu stehen, durch den Regen rennt?
Eine anschauliche Lösung findet sich in den beiden Bildern:
Das obere Bild 1 zeigt die Situation mit stehendem Körper, das untere Bild 2 zeigt das ganze mit einem bewegten Körper. Eingezeichnet sind die "Regenschatten", die die jeweiligen Körper hinterlassen. Die Fläche dieses Regenschattens entspricht der Menge des "abbekommenen" Regens.
Die Körper (Höhe:H, Länge:L) sind die dunkelvioletten Rechtecke. Der Regen ist in seinem Fall durch die senkrechte Straffur dargestellt. Die sich ergebenden Abschattungen sind schrägschraffiert eingezeichnet.
Der Körper in oberen Bild 1 steht in der betrachteten Zeit (t) unbeweglich im Regen. Im unteren Bild 2 bewegt sich der Körper in der gleichen Zeit um die Wegstrecke D. Der Regen fällt in ebenjener Zeit die Wegstrecke Fallstrecke (oben wie unten).
Die Schattenfläche des stehenden Körpers in Bild 1 entspricht den Flächen A1(K1) + A2(K1).
Im Fall des bewegten Körpers aus Bild 2 ergibt sich die Schattenfläche aus "A1(K2)" + "A2(K2)" + "A3".
Wie leicht zu erkennen ist, sind die Größen der violetten Flächen (A1,A2) in beiden Bildern identisch. In Bild 2 ist in der Gesamtabschattungsfläche jedoch zusätzlich noch die Fläche "A3" enthalten. Die Abschattungsfläche des bewegten Körpers ist also größer als die des stehenden Körpers.
Das wäre also geklärt: Man wird nasser, wenn man sich im Regen bewegt ...
techomatic - 2011-10-15 22:54
2 Kommentare - Kommentar verfassen - 0 Trackbacks
Florian (Gast) - 2011-10-16 21:32
Naja
Mag ja stimmen, beides konvergiert aber gegen unendlich. Wenn man jetzt allerdings annimmt, dass man sich bewegen muss um aus dem Regen raus zu kommen so ist die abbekommene Regenmenge im zweiten Fall endlich im ersten Fall aber immer noch unendlich.
Techomatic (Gast) - 2011-10-17 03:04
Also gehe doch einfach davon aus, a) Deine Lebenszeit ist endlich (unglaublich!) und b) die nächste Unterstellmöglichkeit ist bis zum Ende des Regens nicht erreichbar :)
Trackback URL:
//sysout.twoday.net/stories/43005762/modTrackback